Description
Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.
(i.e., 0 1 2 4 5 6 7 might become 4 5 6 7 0 1 2).
You are given a target value to search. If found in the array return its index, otherwise return -1.
You may assume no duplicate exists in the array.
Discussion
这道题可以采用二分查找法。和在一个有序的数组里查找指定元素类似。
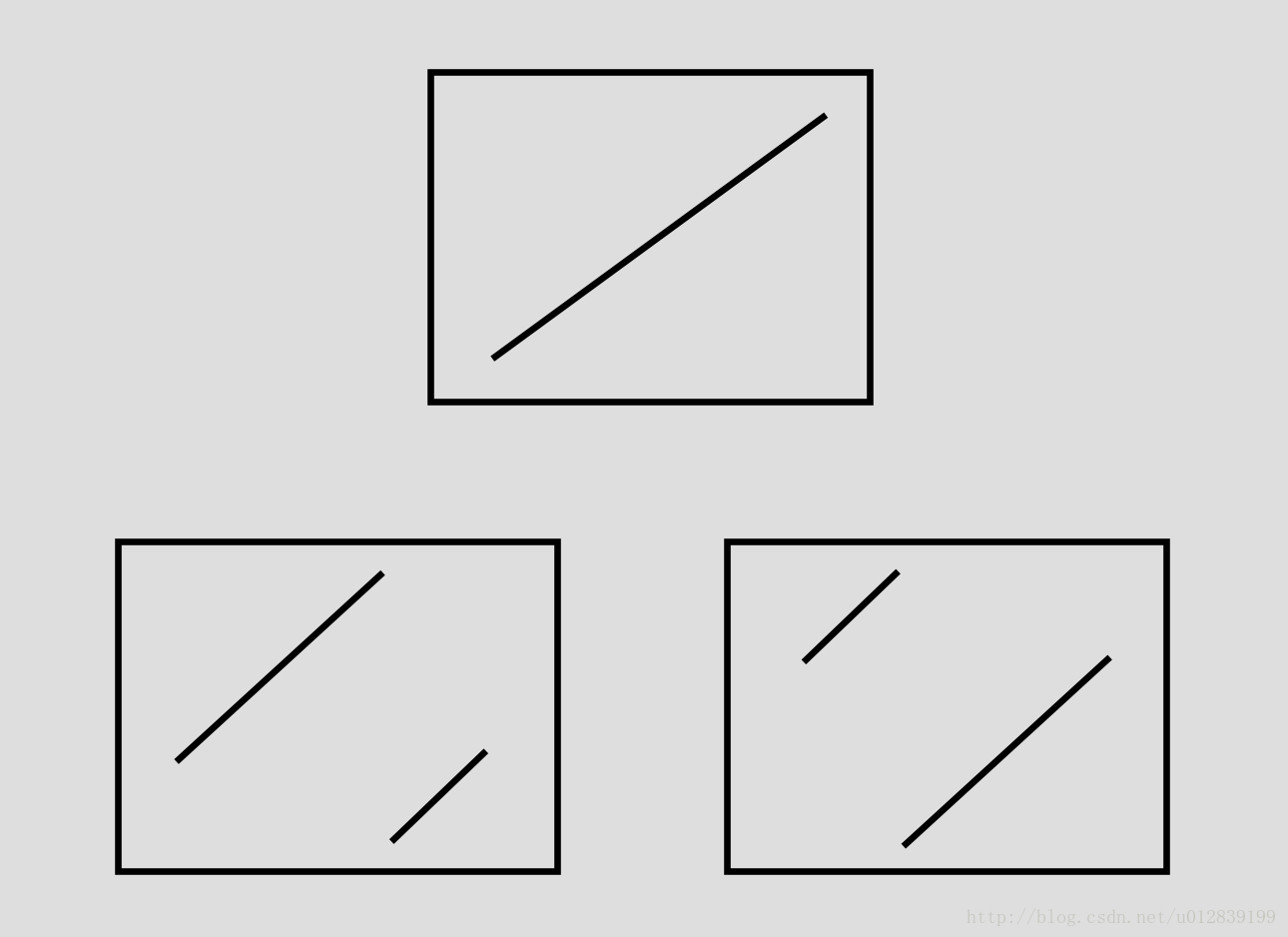
如上图所示,有三种情况。
- nums[leftPos] < nums[rightPos]
- nums[middlePos] > nums[leftPos]:此时可以判定target是否在middle左边。
- nums[middlePos] < nums[rightPos]:此时可以判定target是否在middle右边。
算法的时间复杂度为O(logn)。
C++ Code
class Solution {
public:
int search(vector<int>& nums, int target) {
if(nums.size() == 0)
{
return -1;
}
return binarySearch(nums, target, 0, nums.size() - 1);
}
//二分查找
int binarySearch(vector<int> & nums, int target, int leftPos, int rightPos)
{
int middlePos = (leftPos + rightPos) / 2;
if(nums[leftPos] == target)
{
return leftPos;
}
if(nums[middlePos] == target)
{
return middlePos;
}
if(nums[rightPos] == target)
{
return rightPos;
}
if(rightPos - leftPos <= 2)
{
return -1;
}
//第一种情况 从左向右递增
if(nums[leftPos] < nums[rightPos])
{
if(target > nums[rightPos] || target < nums[leftPos])
{
return -1;
}
if(target > nums[middlePos])
{
return binarySearch(nums, target, middlePos + 1, rightPos - 1);
}
else
{
return binarySearch(nums, target, leftPos + 1, middlePos - 1);
}
}
//第二种情况 middle左侧递增,右侧两段
if(nums[middlePos] > nums[leftPos])
{
if(target > nums[leftPos] && target < nums[middlePos])
{
return binarySearch(nums, target, leftPos + 1, middlePos - 1);
}
else
{
return binarySearch(nums, target, middlePos + 1, rightPos - 1);
}
}
//第三种情况 middle右侧递增,左侧两端
if(nums[middlePos] < nums[rightPos])
{
if(target > nums[middlePos] && target < nums[rightPos])
{
return binarySearch(nums, target, middlePos + 1, rightPos - 1);
}
else
{
return binarySearch(nums, target, leftPos + 1, middlePos - 1);
}
}
return -1;
}
};